Определить принадлежность точки с координатами (x, y) заштрихованной части плоскости.
Для y
[-2,5;2,5] вычислить b=1+|y-x|+0,5*(y-x)2.
Значение x произвольное. Шаг изменения переменной y равен 0,1.
Даны действительные числа a, b, c (a не равно 0). Полностью исследовать биквадратное уравнение
ax4+bx2+c=0.
Если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре корня.
Для x 
[-5,7;5,7] вычислить
Шаг изменения x равен 0,5. Значения x и y вывести в виде таблицы. Найти минимальное значение y на данном интервале.
Даны действительное число a и натуральное n. Вычислить:
| 1 1 1 — + ——— + ... + —————— . a a(a+1) a(a+1)...(a+n) |
Вычислить
Даны действительные числа a, b. Последовательность x1, x2, ..., xn-1, xn образована по закону xn=a+b*cos(0,5*n). Найти первый член последовательности, удовлетворяющий условию |xn-xn-1|< e.
Даны действительные числа x, e. Вычислить с точностью до e
2. Одномерные массивы
Даны натуральное число n , действительные числа a1, а2, ..., аn . Вычислить a12 + a22 + … + an2 .
Дано натуральное число n. Получить последовательность b1, b2, … bn:
bi = 1 + 1/2 + ... + 1/i,
где i=1, 2, …, n.
Даны натуральное число n, действительные числа a1, а2, ... , аn. Получить
max(a1, a1 + а2, a1 + а2 + а3, ... ,a1 + a2 + ... + an).
Даны натуральное число n, целые числа a1, ..., аn (в последовательности могут быть повторяющиеся члены). Получить все числа, которые входят в последовательность по одному разу.
Даны натуральное число n, действительные числа x1, x2, ... , xn. Получить в порядке следования все xk, удовлетворяющие неравенствам xk>x1, xk>x2, ... ,xk>xk-1.
Даны целые числа a1, ..., an, каждое из которых отлично от 0. Если в последовательности отрицательные и положительные члены чередуются (+,-,+,-,.. или -,+,-,+,...), то ответом должна служить исходная последовательность. Иначе получить все отрицательные члены, сохранив порядок их следования.
3. Двумерные массивы
В данной действительной квадратной матрице порядка n найти сумму элементов строки, на которой расположен элемент с наименьшим значением.
Дан массив a1, a2, ..., an. Отсортитовать массив по возрастанию, используя следующий алгоритм: последовательном просмотром чисел a1, a2, ..., an найти наименьшее i, такое , что аi > аi-1. Поменять местами аi и ai-1 и возобновить просмотр с начала массива. Когда не удастся найти такое i, массив будет упорядочен нужным образом.
Дана вещественная квадратная матрица порядка n . Удалить из неё i-ю строку и j-й столбец. Для поиска нужной строки и столбца, а также для сжатия матрицы использовать подпрограмму.
Даны действительные числа a1, а2, ..., а64. Получить действительную квадратную матрицу порядка 8, элементами которой являются данные числа, расположенные в ней по схеме.
Схема
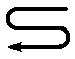
4. Строки
Даны натуральное число n, символы s1, s2, ... ,sn. Заменить в этой последовательности каждую группу букв child группой букв children.
Дана строка символов, среди которых есть хотя бы одна точка. Преобразовать строку, удалив из нее все запятые, предшествующие первой точке.
Составить программу упорядочивания слов по алфавиту. Множество слов представлено в виде строки символов заданного размера. Слова в строке отделены символом пробел.
Багаж пассажира характеризуется количеством вещей и их общим весом. Дан массив, содержащий информацию о багаже нескольких пассажиров. Определить, имеются ли два пассажира, багажи которых совпадают по числу вещей и различаются по весу не более чем на 0.5 кг.
Сведения о служащих содержат фамилию , адрес, дату приема на работу, годовой заработок и номер отдела. Вывести данные о служащих, работающих в пятом отделе.